Содержание страницы:
Закон больших чисел в примерах
Основными понятиями теории вероятностей являются понятия случайного события и случайной величины. При этом предсказать заранее результат испытания, в котором может появиться или не появиться то или иное событие или какое-либо определенное значение случайной величины, невозможно, так как исход испытания зависит от многих случайных причин, не поддающихся учету.
Однако при неоднократном повторении испытаний наблюдаются закономерности, свойственные массовым случайным явлениям. Эти закономерности обладают свойством устойчивости. Суть этого свойства состоит в том, что конкретные особенности каждого отдельного случайного явления почти не сказываются на среднем результате большой массы подобных явлений, а характеристики случайных событий и случайных величин, наблюдаемых в испытаниях, при неограниченном увеличении числа испытаний становятся практически не случайными.
Пусть производится большая серия однотипных опытов. Исход каждого отдельного опыта является случайным, неопределенным. Однако, несмотря на это, средний результат всей серии опытов утрачивает случайный характер, становится закономерным.
Для практики очень важно знание условий, при выполнении которых совокупное действие очень многих случайных причин приводит к результату, почти не зависящему от случая, так как позволяет предвидеть ход явлений. Эти условия и указываются в теоремах, носящих общее название закона больших чисел.
Под законом больших чисел не следует понимать какой-то один общий закон, связанный с большими числами. Закон больших чисел — это обобщенное название нескольких теорем, из которых следует, что при неограниченном увеличении числа испытаний средние величины стремятся к некоторым постоянным.
К ним относятся теоремы Чебышева и Бернулли. Теорема Чебышева является наиболее общим законом больших чисел, теорема Бернулли — простейшим.
В основе доказательства теорем, объединенных термином «закон больших чисел», лежит неравенство Чебышева, по которому устанавливается вероятность отклонения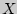 
от ее математического ожидания:
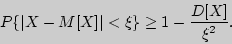
Пример 81. Устройство состоит из 100 независимо работающих элементов. Вероятность отказа каждого элемента за время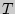 
равна 0,03. Оценить вероятность того, что абсолютная величина разности между числом (математическом ожиданием) отказов за время 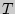окажется: а) меньше двух; б) не меньше двух.
Решение. а). Обозначим через 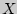число отказавших элементов за время 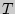. Тогда 
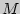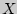[] = np = 100 ? 0,03 = 3 и 
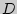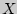[] = npq = 100 ? 0,03 ? 0,97 = 2,91 (см. пример ). Воспользуемся неравенством Чебышева:
подставив в него 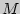[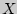] = 3, 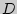[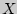] = 2,91, 
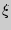= 2, получим
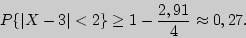
б). События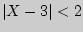 
и 
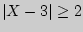противоположны, поэтому сумма их вероятностей равна единице. Следовательно,
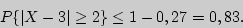
Пример 82. Оценить вероятность события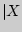 
— [] 
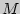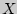0?
168. Каждая из 1000 независимых случайных величин имеет дисперсию, равную 4, а математические ожидания их одинаковы. Оцените вероятность того, что среднее арифметическое случайных величин отклонится от математического ожидания по абсолютной величине не более чем на 0,1.
III 169. Применима ли к последовательности случайных величин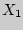 
, 
, . 
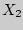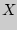, . имеющих равномерное распределение в промежутке ]
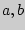[, теорема Чебышева?
170. Пусть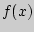 
> 0 — неубывающая функция. Доказать, что если существует [ 
(
[]
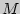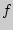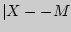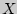], то
Энциклопедия заблуждений
собрание невероятных фактов, удивительных открытий и опасных поверий
Недавние статьи
Закон больших чисел
Posted on | November 21, 2011 | 2 Comments
Частные определенные события или совпадения произойдут с малой вероятностью. Некоторые удивительные неопределенные события произойдут наверняка. Вот почему замечательные совпадения отмечаются задним числом, а не предсказываются. – Д. Майерс
Закон больших чисел говорит, что при достаточно большой выборке очень вероятны совпадения.
Например, вы можете быть в восторге от человека, который выиграл в лотерею два раза, считая, что повторные шансы на победу являются астрономическими. Нью-Йорк Таймс поместила статью о женщине из Нью-Джерси, которая выиграла в лотерею дважды, называя ее шансы “1 из ??17 трлн”. Тем не менее, статистики Stephen Samuels и George McCabe из Университета Пердью вычислили шансы выиграть в лотерею два раза и получили примерно 1 шанс из 30 за четыре месяца и они лучше, чем шансы за период семь лет. Почему? Потому что игроки не покупают один билет для каждой из двух лотерей, они покупают несколько билетов каждую неделю (Diaconis and Mosteller).
Некоторые люди сочтут удивительным, что 16 млн. человек на планете имеют дату рождения, которая совпадает с их собственной. На обычном футбольном матче с 50 000 болельщиков, большинство фанатов разделяет свой день рождения еще с примерно 135 другими присутствующими. (Исключение будет для тех, кто родился 29 февраля. У них будет только около 34 совпадений даты рождения.)
Вы можете счесть еще более поразительным, что “в случайной выборке из двадцати трех человек, есть 50-процентный шанс, что хотя бы два из них отмечают одну и ту же дату рождения” (Martin ).
С другой стороны, вы можете сказать, что шансы некоторого события миллион к одному. Вы будете поражены , но такие шансы так же велики, как случайность или совпадение. С более чем 6 миллиардов человек на Земле, одно совпадение на миллион будет происходить достаточно часто. Скажите шансы миллион к одному, что когда человеку приснится авиакатастрофа, она произойдет на следующий день. С 6 миллиардов людей, имеющих в среднем 250 сновидений за ночь (Hines говорит о 50, хотя я не думаю, что я когда-либо имел более 5 или 6 сновидений за ночь), должно быть от 30 тысяч до 1,5 миллиона человек каждый день, кто видит “вещие сны” . Число на самом деле будет больше, так как мы склонны видеть во сне вещи, которые нас беспокоят и данные сны, как правило, расплывчаты или неоднозначны, что дает широкий диапазон событий, подразумевающих выполнение наших мечтаний.
Карл Юнг, как и многие люди, которые испытали сверхъестественное сопряжение событий, не думал, что такие случаи являются простыми совпадениями. Он разработал понятие синхронности для объяснения “значимых совпадений”. Он описал, как синхронность акаузальный принцип, который связывает события, имеющие аналогичный смысл при совпадение по времени. Однако, если подумать обо всех парных событиях, что могут случиться в жизни человека, и добавить к этому наше универсальное умение находить причинные связи между вещами, то тогда будет большая вероятность, что большинство из нас будет испытывать много значимых совпадений. Совпадения предсказуемы, и мы сами придаем им смысл. Учитывая тот факт, что на Земле миллиарды людей и возможное число значимых совпадений миллионы миллиардов, многие люди неизбежно будут испытывать некоторые очень странные и сверхъестественные совпадения каждый день.
Наконец, кластеры совпадений могут показаться разработанными или с заранее предопределенным результатом для тех, кто очень селективен в своем мышлении, как например Ури Геллер . После антиамериканских террористических актов 11 сентября 2001 года, Геллер разместил свое мысли о числе 11. Он попросил всех молиться за одиннадцать секунд для тех, кто нуждается. Почему? Он был убежден, что было зашифрованное, нумерологическое сообщение в событиях, которые произошли в этот день. На самом деле, он признает, что у него были длительные отношения с числом 11 . Он считает, что 11 “отображает позитивную связь и шлюз к тайнам Вселенной и за ее пределы.” Но вот то, что он должен был сказать о теракте и как 11 относится и по сей день позора:
Тайна числа 11 Ури Геллера
* 119, код города в Ирак / Иран. 1 + 1 + 9 = 11 (обратный номера и у вас есть дата) [ошибка: код страны Ирана 98 (9 +8 = 17), Ирак 964 ( 9 +6 +4 = 19);. код Саудовской Аравии 966 (9 +6 +6 = 21)]
*Башни-близнецы – стоя бок о бок, выглядят как число 11
*Первым самолетом, который ударил башни был Рейс 11
*American Airlines или АА – 1-я буква в алфавите, поэтому снова 11:11
* штат Нью-Йорк – 11-м добавлен в Союз
*Нью-Йорк Сити – 11 букв
* USS Enterprise находился в северной части Мексиканского залива во время нападения, а его корабельный номер 65N 6 +5 = 11 [возможно что нет. Я получил следующее письмо: “Мы были на самом деле около 12 часов от экватора (я знаю это, потому что мы собирались пересечения церемониальную линию ночью) на нашем пути в Южную Африку мы покинули залив.”]
* Рейс 11 – 92 на борту – 9 + 2 = 11
* Рейс 77 – 65 на борту – 6 + 5 = 11
* # истории 110 (2x) 110 – 110 Помните, что ноль “0” не является числом, поэтому мы имеем 11:11
* дом, где они предположительно жили был # 10001 ноль не считаем
Названия, которые имеют одиннадцать букв
* Air Force One, * Джордж Буш * Билл Клинтон, * Саудовская Аравия, * Второй мировой терроризм, * Колин Пауэлл *День памяти 11 ноября * Ноябрь также 11 месяц
* Мохаммед Атта , пилот, который врезался в Центре Международной Торговли.
Геллер также утверждал, что “будет больше информации” и призвал читателей присылать ему на электронную почту как можно больше результатов такого рода. Геллер также написал: “Я хотел бы призвать каждого отправить это сообщение всем членам Вашей семьи, друзьям или деловым знакомым и попытаться поставить это в правильную перспективу”.
Позвольте мне попытаться поместить это в правильную перспективу.
Накопление большего количества совпадений между числом 11 и другими вещами очень легкое дело, поскольку есть бесчисленное множество предметов, которые могут быть связаны каким-либо образом, чтобы получить число 11 (или 12, 13, или любое другое число или слово ) . Например, код страны Пакистана 92 (9 + 2 = 11), Boeing 757 вмещает около 11 тысяч галлонов топлива и размах крыльев 155 футов (1+ 5+ 5 = 11), Нострадамус и Билли Грэм имеют 11 букв, перед любым словом из 8 букв просто поместите артикль “the”; перед любым словом из 9 букв, просто поставьте ww или любое слово из двух букв, перед любым словом из 10 букв поместите артикль “а” или “s” с конца, и т.д. Это особенно легко сделать, так как нет конкретного руководства, прежде чем мы начнем нашу охоту на удивительные факты относительно того, что будет и что не будет считаться релевантным. У нас есть почти безграничное множество предметов, которые будут “попаданиями”. К сожалению для Геллера и других, которые находятся под впечатлением попаданий, есть и еще более широкий круг предметов, которые будут промахами. Геллер не видит их, потому что он не ищет их.
Если мы начнем охоту на пункты, которые будут релевантными, но не будут соответствовать шаблону, мы скоро увидим, что нет ничего особенного в списке Геллера или числе 11. Только путем сосредоточения внимания на всем, что соответствует нашей вере и игнорируя все, что не подходит, мы можем сделать эти совпадения значимыми.
Закон больших чисел
Совокупность всех договоров страхования, заключенных компанией, называют страховым портфелем. По каждому договору существует риск наступления убытка. То есть выплата по договору является случайной величиной. Страховой портфель представляет собой множество таких случайных величин.
В рамках теории вероятностей изучены общие закономерности, которым подчиняются множества случайных событий. В частности, доказано, что совокупное действие большого количества случайных величин при соблюдении некоторых условий приводит к результату, почти не зависящему от случая. Теоремы, описывающие указанную закономерность, носят общее название «закон больших чисел».
Подобное «неслучайное» поведение результата воздействия большого числа случайных величин может быть объяснено взаимной компенсацией их отклонений от некоторого ожидаемого «среднего» значения. Например, результат страхования по любому конкретному договору является случайным. Если сумма выплат по нему окажется меньше уплаченной премии, для страховой компании результат будет положительным. В противном случае — отрицательным. Но в рамках коллектива договоров суммирование подобных положительных и отрицательных отклонений уменьшает разброс общего результата по портфелю. Совокупный итог страховых операций утрачивает случайный характер, становится более предсказуемым, закономерным. В этом проявляется эффект так называемого коллективного баланса.
При установлении платы за страхование очень важно правильно определить цену риска, который передает участник в фонд. Согласно закону больших чисел для значительной совокупности рисков сумма убытков будет с высокой вероятностью стремиться к своему ожидаемому значению. Это означает, что при расчете цены страхования для количественной оценки риска можно использовать ожидаемые значения выплат.
Пример. Объединение рисков
Предположим, что вероятность хищения автомобиля определенной марки стоимостью 500 ООО руб. составляет 0,03 в год (т.е. в среднем угоняют три автомобиля из 100). Возможность хищения существует всегда. И хотя оно происходит лишь с 3% автовладельцев, для каждого их них это событие может стать катастрофой. По существу, данный риск представляет «игру», где с вероятностью 3% можно проиграть 500 000 руб., но нельзя выиграть. Поэтому вполне логично, что люди хотят иметь защиту от таких событий.
Если автовладелец хочет защититься самостоятельно, он должен создать запас средств для компенсации убытков, т.е. для приобретения нового автомобиля. Сколько денег необходимо отложить, чтобы быть уверенным в защите? Для индивидуального владельца ответ очевиден — 500 000 руб. Любой другой суммы, меньшей, чем эта, на покупку аналогичной машины просто не хватит. Но далеко не все могут создать такой резерв.
Теперь допустим, что 1000 автомобилистов решили создать объединенный страховой фонд для выплат тем, у кого угнали автомобиль. В соответствии с законом больших чисел средняя частота хищений в данном коллективе рисков с высокой вероятностью будет стремиться к своему теоретическому значению 0,03. То есть на 1000 машин будет ожидаться 30 угонов. Если разделить общую стоимость автомобилей, которые предположительно будут похищены, на всех участников, то с каждого достаточно будет собрать 500 000 o 30/1000 = 15 000 руб.! За эту плату автовладелец вправе ожидать полного возмещения убытка в размере 500 000 руб.
При таком способе защиты участник фонда жертвует относительно небольшой (по сравнению с возможным убытком) суммой в обмен на уверенность, что при хищении ему возместят стоимость автомобиля. Это стало возможным в результате объединения значительного количества участников, подверженных одному риску, в один страховой фонд, результаты деятельности которого становятся почти неслучайными благодаря действию закона больших чисел.
В реальной жизни объединиться и правильно рассчитать экономику деятельности фонда такому большому числу людей практически невозможно. Поэтому страховые фонды создаются и управляются специальными страховыми организациями — коммерческими страховыми компаниями и некоммерческими обществами взаимного страхования.
При использовании закона больших чисел для объединения даже огромного числа случайных величин следует понимать, что он не гарантирует равенство наблюдаемых средних результатов ожидаемым теоретическим значениям. Закон позволяет лишь говорить о том, что для больших множеств серьезные относительные отклонения фактических результатов от ожидаемых значений менее вероятны. Для крупных объединений рисков возможная сумма убытков более предсказуема, чем для малых. Поэтому рост количества договоров в портфеле страховой компании необходим прежде всего для обеспечения надежности.
Для оценки риска необходимо знать вероятности и ожидаемые суммы убытков. Но объективно существующие теоретические значения этих параметров неизвестны. Имеются лишь данные о страховых случаях за прошлые годы, которые представляют собой результаты реализации изучаемых случайных событий. Если их достаточно много, то согласно закону больших чисел наблюдаемые средние значения почти наверняка будут близки к ожидаемым. Тем самым закон дает возможность использовать статистические данные для оценки вероятностей наступления рисков и ожидаемых значений убытков.
Таким образом, применительно к страхованию закон больших чисел теоретически обосновывает:
— возможность применения для оценки риска ожидаемых значений;
— необходимость увеличения количества договоров в портфеле для уменьшения относительных отклонений результатов и обеспечения стабильности страхового фонда;
— возможность использования статистических данных для оценки вероятностей и сумм убытков.
Подчеркивая такое широкое применение положений закона больших чисел к страховым задачам, его часто называют фундаментальным законом страхования.
Закон больших чисел
Взаимодействуя ежедневно в работе или учебе с цифрами и числами, многие из нас даже не подозревают о том, что существует очень интересный закон больших чисел, применяемый, например, в статистике, экономике и даже психолого-педагогических исследованиях. Он относится к теории вероятностей и говорит о том, что среднее арифметическое какой-либо большой выборки из фиксированного распределения близко к математическому ожиданию этого распределения.
Вы, наверное, заметили, что понять сущность этого закона непросто, особенно тем, кто не особо дружит с математикой. Исходя из этого, мы бы хотели рассказать о нем простым языком (насколько это возможно, конечно), чтобы каждый мог хотя бы примерно уяснить для себя, что это такое. Эти знания помогут вам лучше разобраться в некоторых математических закономерностях, стать более эрудированным и положительным образом повлиять на развитие мышления.
Понятия закона больших чисел и его трактовка
Помимо рассмотренного нами выше определения закона больших чисел в теории вероятностей, можно привести и его экономическое толкование. В этом случае он представляет собой принцип, согласно которому частоту финансовых потерь конкретного вида можно предсказать с высокой степенью достоверности тогда, когда наблюдается высокий уровень потерь подобных видов вообще.
Помимо этого, в зависимости от уровня сходимости признаков можно выделить слабый и усиленный законы больших чисел. О слабом речь идет, когда сходимость существует по вероятности, а об усиленном – когда сходимость существует практически во всем.
Если интерпретировать несколько иначе, то следует сказать так: всегда можно найти такое конечное число испытаний, где с любой запрограммированной наперед вероятностью меньше единицы относительная частота появления какого-то события будет крайне мало отличаться от его вероятности.
Таким образом, общую суть закона больших чисел можно выразить так: результатом комплексного действия большого количества одинаковых и независимых случайных факторов будет такой результат, который не зависит от случая. А если говорить еще более простым языком, то в законе больших чисел количественные закономерности массовых явлений будут явно проявляться только при большом их числе (поэтому и называется закон законом больших чисел).
Отсюда можно сделать вывод, что сущность закона состоит в том, что в числах, которые получаются при массовом наблюдении, имеются некоторые правильности, обнаружить которые в небольшом количестве фактов невозможно.
Сущность закона больших чисел и его примеры
Закон больших чисел выражает наиболее общие закономерности случайного и необходимого. Когда случайные отклонения «гасят» друг друга, средние показатели, определенные для одной и той же структуры, приобретают форму типичных. Они отражают действия существенных и постоянных фактов в конкретных условиях времени и места.
Определенные посредством закона больших чисел закономерности сильны только тогда, когда представляют массовые тенденции, и они не могут быть законами для отдельных случаев. Так, вступает в силу принцип математической статистики, говорящий, что комплексное действие ряда случайных факторов способно стать причиной неслучайного результата. И наиболее яркий пример действия данного принципа – это сближение частоты наступления случайного события и его вероятности, когда возрастает количество испытаний.
Давайте вспомним обычное бросание монетки. Теоретически орел и решка могут выпасть с одной и той же вероятностью. Это означает, что если, к примеру, бросить монетку 10 раз, 5 из них должна выпасть решка и 5 – орел. Но каждый знает, что так не происходит практически никогда, ведь соотношение частоты выпадения орла и решки может быть и 4 к 6, и 9 к 1, и 2 к 8 и т.д. Однако с увеличением количества подбрасываний монетки, например, до 100, вероятность того, что выпадет орел или решка, достигает 50%. Если же теоретически проводить бесконечное количество подобных опытов, вероятность выпадения монетки обеими сторонами всегда будет стремиться к 50%.
На то, как именно упадет монетка, влияет огромное число случайных факторов. Это и положение монетки на ладони, и сила, с которой совершается бросок, и высота падения, и его скорость и т.д. Но если опытов много, вне зависимости от того, как воздействуют факторы, всегда можно утверждать, что практическая вероятность близка к вероятности теоретической.
А вот еще один пример, который поможет понять сущность закона больших чисел: предположим, что нам нужно оценить уровень заработка людей в каком-то регионе. Если мы будем рассматривать 10 наблюдений, где 9 человек получают 20 тыс. рублей, а 1 человек – 500 тыс. рублей, среднее арифметическое составит 68 тыс. рублей, что, естественно, маловероятно. Но если мы возьмем в расчет 100 наблюдений, где 99 человек получают 20 тыс. рублей, а 1 человек – 500 тыс. рублей, то при расчете среднего арифметического получим 24,8 тыс. рублей, что уже ближе к реальному положению дел. Увеличивая число наблюдений, мы будем заставлять среднее значение стремиться к истинному показателю.
Именно по этой причине для применения закона больших чисел в первую очередь необходимо набрать статистический материал, чтобы получать правдивые результаты, изучая большое число наблюдений. Потому-то и удобно использовать этот закон, опять же, в статистике или социальной экономике.
Подведем итоги
Значение того, что закон больших чисел работает, сложно переоценить для любой области научного знания, и особенно для научных разработок в области теории статистики и методов статистического познания. Действие закона также обладает большим значением и для самих изучаемых объектов с их массовыми закономерностями. На законе больших чисел и принципе математической статистике основываются практически все методы статистического наблюдения.
Но, даже не беря во внимание науку и статистику как таковые, можно смело сделать вывод, что закон больших чисел – это не просто явление из области теории вероятностей, но феномен, с которым мы сталкиваемся практически каждый день в своей жизни.
Надеемся, теперь сущность закона больших чисел стала вам более понятна, и вы сможете легко и просто объяснить его кому-то другому. А если тема математики и теории вероятностей вам интересна в принципе, то рекомендуем почитать о числах Фибоначчи и парадоксе Монти Холла. Также познакомьтесь с приближенными вычислениями в жизненных ситуациях и самыми популярными числами. И, конечно же, обратите внимание на наш курс по когнитивистике, ведь, пройдя его, вы не только овладеете новыми техниками мышления, но и улучшите свои когнитивные способности в целом, в том числе и математические.
Закон больших чисел. Неравенство Чебышева
Закон больших чисел. Неравенство Чебышева
- Услуги проектирования
- Теория вероятности
- Закон больших чисел. Неравенство Чебышева
Закон больших чисел. Неравенство Чебышева
Закон больших чисел
При многократном повторении испытаний, массовые случайные явления могут проявляться с определёнными закономерностями. Эти закономерности обладают свойством устойчивости, суть которого состоит в том, что действие отдельной случайной величины почти не влияет на среднее значение большого числа подобных величин.
Для практики важно знать условия > , в результате которых действие многих случайных величин приводит к результату почти не зависимому от случая. Эти условия или эту зависимость между случайностью и закономерностью устанавливают предельные теоремы вероятностей.
Под законом больших чисел не следует понимать какой-то один общий закон, связанный с большими числами. Закон больших чисел — это обобщённое название нескольких теорем из которых следует, что при неограниченном увеличении числа испытаний, среднее значение этих величин стремится к некоторым постоянным числам.
По смыслу эти теоремы можно разбить на две группы. Одна группа — закон больших чисел < теоремы Чебышева, Бернулли >, другая — центральная предельная теорема
Для доказательства этих теорем потребуется неравенство Чебышева.
Неравенство Чебышева
Неравенство Чебышева справедливо для дискретных и непрерывных случайных величин. Пусть у нас есть дискретная случайная величина, заданная рядом распределения.
$ \begin < l|l|l|l|l|l >X & X_1 & X_2 & X_3 & \cdots & X_n \\ \hline P & P_1 & P_2 & P_3 & \cdots & P_n \end $
Требуется оценить вероятность того, что отклонение случайной величины от её математического ожидания не превышает по абсолютной величине положительного числа $\xi$.
Теорема < неравенство Чебышева >. Для произвольной случайной величины X с математическим ожиданием a=M(X) и дисперсией $\sigma ^2=D( x )$, для любого $\xi >0$ справедливо равенство \begin \label < eq2 >P( < \left| < x-a >\right|>\xi > )\leqslant \frac < \sigma ^2 > < \xi ^2 >\qquad (2) \end
\begin \label < eq3 >P( < \left| < x-a >\right|\leqslant \xi > )\geqslant 1-\frac < \sigma ^2 > < \xi ^2 >\qquad (3) \end
Из неравенства Чебышева следует — чем меньше $D(x)$, тем меньше вероятность отклонения. Неравенство Чебышева применимо для любых случайных величин. В форме < 1 >оно устанавливает верхнюю границу, а в форме < 3 >— нижнюю границу вероятности рассматриваемого события.
Запишем неравенство Чебышева в форме < 3 >для случайной величины Х имеющей биномиальный закон распределения с математическим ожиданием $а=M < X >=np$ и дисперсией $D(X)=npq$.
В основном неравенство Чебышева имеет теоретическое значение для теорем.
Пример. Средний расход воды на ферме составляет 1000л. в день, а среднее квадратическое отклонение этой случайной величины не превышает 200л. Оценить вероятность того, что расход воды на ферме в любой выбранный день не превзойдет 2000л.
Решение. Пусть $X$ — расход воды на ферме. По условию $M(x)=1000$. Дисперсия $D(x)=\sigma ^2\leqslant 200^2$. Так как границы интервала $0\leqslant X\leqslant 2000$ симметричны относительно математического ожидания $M(x)=1000$, то для оценки вероятности искомого события применим неравенство Чебышева:
$P(X\leqslant 2000)=P(0\leqslant X\leqslant 2000)=P( < \left| < X-1000 >\right|\leqslant 1000 > )\geqslant 1-\frac < 200^2 > < 1000^2 >=0,96$, т.е. не менее, чем 0,96.
Формула Гаусса — Остроградского
Несобственные интегралы от неограниченной функции
Дифференциальные характеристики векторного поля
Полином Жегалкина. Теорема о представлении в виде полинома Жегалкина
Условия независимости криволинейного интеграла от пути интегрирования
Решение задач с помощью алгебры высказываний
Определение криволинейного интеграла второго рода
Поток векторного поля через поверхность
Вычисление площадей плоских областей
Скалярное поле, производная по направлению, градиент
Гармонические поля
Лемма о построении множества $[F]_$
Булевы функции от $n$ переменных
Вычисление криволинейного интеграла второго рода. Примеры.
Примеры применения цилиндрических и сферических координат
Огравление $\Rightarrow $