Содержание страницы:
Правила для построения сечений
Правила построения сечений многогранников:
1) проводим прямые через точки, лежащие в одной плоскости;
2) ищем прямые пересечения плоскости сечения с гранями многогранника, для этого
а) ищем точки пересечения прямой принадлежащей плоскости сечения с прямой, принадлежащей одной из граней (лежащие в одной плоскости);
б) параллельные грани плоскость сечения пересекает по параллельным прямым.
Примеры построения сечений:
Рассмотрим прямоугольный параллелепипед ABCDA1B1C1D1. Построим сечение, проходящее через точки M, N, L.

Соединим точки M и L, лежащие в плоскости AA1D1D.

Пересечем прямую ML ( принадлежащую сечению) с ребром A1D1, они лежат в одной плоскости AA1D1D. Получим точку X1.

Точка X1 лежит на ребре A1D1, а значит и плоскости A1B1C1D1, соединим ее сточкой N, лежащей в этой же плоскости.
X1 N пересекается с ребром A1B1 в точке К.

Соединим точки K и M, лежащие в одной плоскости AA1B1B.

Найдем прямую пересечения плоскости сечения с плоскостью DD1C1C:
пересечем прямую ML (принадлежащую сечению) с ребром DD1, они лежат в одной плоскости AA1D1D, получим точку X2;

пересечем прямую KN (принадлежащую сечению) с ребром D1C1, они лежат в одной плоскости A1B1C1D1, получим точку X3;

Точки X2 и X3 лежат в плоскости DD1C1C. Проведем прямую X2 X3 , которая пересечет ребро C1C в точке T, а ребро DC в точке P. И соединим точки L и P, лежащие в плоскости ABCD.

MKNTPL — искомое сечение.
Рассмотрим ту же самую задачу на построение сечения, но воспользуемся свойством параллельных плоскостей. Это облегчит нам построение сечения.
 .
.
Соединим точки M и L, лежащие в плоскости AA1D1D.
 .
.
Через точку N, проведем прямую NT параллельную прямой ML. Прямые NT и ML лежат в параллельных плоскостях по свойству параллелепипеда.
 .
.
Пересечем прямую ML ( принадлежащую сечению) с ребром A1D1, они лежат в одной плоскости AA1D1D. Получим точку X1.
 .
.
Точка X1 лежит на ребре A1D1, а значит и плоскости A1B1C1D1, соединим ее сточкой N, лежащей в этой же плоскости.
X1 N пересекается с ребром A1B1 в точке К.
 .
.
Соединим точки K и M, лежащие в одной плоскости AA1B1B.
 .
.
Проведем прямую TP через точку T, параллельно прямой KM ( они лежат в параллельных плоскостях).
 .
.
Соединим точки P и L ( они лежат в одной плоскости).
 .
.
Построение сечений многогранника. 1.Определение сечения. 2.Правила построения сечений. 3.Виды сечений тетраэдра. 4.Виды сечений параллелепипеда. 5.Задача. — презентация
Презентация была опубликована 4 года назад пользователемЯрослав Павлинов
Похожие презентации
Презентация на тему: » Построение сечений многогранника. 1.Определение сечения. 2.Правила построения сечений. 3.Виды сечений тетраэдра. 4.Виды сечений параллелепипеда. 5.Задача.» — Транскрипт:
1 Построение сечений многогранника
2 1.Определение сечения. 2.Правила построения сечений. 3.Виды сечений тетраэдра. 4.Виды сечений параллелепипеда. 5.Задача на построение сечения тетраэдра с объяснением. 6.Решение задачи на построение сечения (с наводящими вопросами). 7.Задача на построение сечения параллелепипеда. 8.Задача на построение сечения параллелепипеда.
3 Секущей плоскостью многогранника называется любая плоскость, по обе стороны от которой имеются точки данного многогранника. L
4 Секущая плоскость пересекает грани многоугольника по отрезкам. Многоугольник, сторонами которого являются данные отрезки, называется сечением многогранника. L
5 1.Определение сечения. 2.Правила построения сечений. 3.Виды сечений тетраэдра. 4.Виды сечений параллелепипеда. 5.Задача на построение сечения тетраэдра с объяснением. 6.Решение задачи на построение сечения (рассмотрение двух вариантов построения). 7.Задача на построение сечения параллелепипеда. 8.Задача на построение сечения параллелепипеда.
6 Правила построения сечений многогранников: 1)проводим прямые через точки, лежащие в одной плоскости; 2) ищем прямые пересечения плоскости сечения с гранями многогранника, для этого: ищем точки пересечения прямой принадлежащей плоскости сечения с прямой, принадлежащей одной из граней (лежащие в одной плоскости); параллельные грани плоскость сечения пересекает по параллельным прямым.
7 1.Определение сечения. 2.Правила построения сечений. 3.Виды сечений тетраэдра. 4.Виды сечений параллелепипеда. 5.Задача на построение сечения тетраэдра с объяснением. 6.Решение задачи на построение сечения (рассмотрение двух вариантов построения). 7.Задача на построение сечения параллелепипеда. 8.Задача на построение сечения параллелепипеда.
8 Какие многоугольники могут получиться в сечении ? Тетраэдр имеет 4 грани В сечениях могут получиться: Четырехугольники Треугольники
9 1.Определение сечения. 2.Правила построения сечений. 3.Виды сечений тетраэдра. 4.Виды сечений параллелепипеда. 5.Задача на построение сечения тетраэдра с объяснением. 6.Решение задачи на построение сечения (рассмотрение двух вариантов построения). 7.Задача на построение сечения параллелепипеда. 8.Задача на построение сечения параллелепипеда.
10 Треугольники Параллелепипед имеет 6 граней Четырехугольники Шестиугольники Пятиугольники В его сечениях могут получиться :
11 1.Определение сечения. 2.Правила построения сечений. 3.Виды сечений тетраэдра. 4.Виды сечений параллелепипеда. 5.Задача на построение сечения тетраэдра с объяснением. 6.Решение задачи на построение сечения (рассмотрение двух вариантов построения). 7.Задача на построение сечения параллелепипеда. 8.Задача на построение сечения параллелепипеда.
12 E F K L A B C D M 1. Проводим КF. 2. Проводим FE. 3. Продолжим EF, продолжим AC. 5. Проводим MK. 7. Проводим EL EFKL – искомое сечение 6. MK AB=L 4. EF AC =М Построить сечение тетраэдра, через точки E, F, K.
13 1.Определение сечения. 2.Правила построения сечений. 3.Виды сечений тетраэдра. 4.Виды сечений параллелепипеда. 5.Задача на построение сечения тетраэдра с объяснением. 6.Решение задачи на построение сечения (рассмотрение двух вариантов построения). 7.Задача на построение сечения параллелепипеда. 8.Задача на построение сечения параллелепипеда.
14 E F K L A B C M D Какие точки можно сразу соединить? С какой точкой, лежащей в той же грани, можно соединить полученную дополнительную точку? Какие прямые можно продолжить, чтобы получить дополнительную точку ? F и K, Е и К ЕК и АС С точкой F Соедините получившиеся точки, лежащие в одной грани, назовите сечение. ЕLFK Второй способ Построить сечение тетраэдра, через точки E, F, K.
15 E F L A B C D О Построить сечение тетраэдра плоскостью, проходящей через точки E, F, K. K Первый способ
16 Вывод: независимо от способа построения сечения одинаковые. Способ 1. Способ 2.
17 1.Определение сечения. 2.Правила построения сечений. 3.Виды сечений тетраэдра. 4.Виды сечений параллелепипеда. 5.Задача на построение сечения тетраэдра с объяснением. 6.Решение задачи на построение сечения (рассмотрение двух вариантов построения). 7.Задача на построение сечения параллелепипеда. 8.Задача на построение сечения параллелепипеда.
18 A1A1 А В В1В1 С С1С1 D D1D1 M N Построить сечения параллелепипеда плоскостью, проходящей через точки В 1, М, N O К Е P 1. MN 2.Продолжим MN,ВА 4. В 1 О 6. КМ 7. Продолжим MN и BD. 9. В 1 E 5. В 1 О А 1 А=К 8. MN BD=E 10. B 1 Е D 1 D=P, PN 3.MN BA=O
19 1.Определение сечения. 2.Правила построения сечений. 3.Виды сечений тетраэдра. 4.Виды сечений параллелепипеда. 5.Задача на построение сечения тетраэдра с объяснением. 6.Решение задачи на построение сечения (рассмотрение двух вариантов построения). 7.Задача на построение сечения параллелепипеда. 8.Задача на построение сечения параллелепипеда.
20 A1A1 А В В1В1 С С1С1 D D1D1 Построить сечение параллелепипеда плоскостью, проходящей через точки M,A,D. М 1. AD 2. MD 3. ME//AD, т.к. (ABC)//(A 1 B 1 C 1 ) 4. AE 5. AEMD – сечение. E
Учимся строить сечения многогранников. Часть 2.
Учимся строить сечения многогранников. Часть 2.
Эта статья для тех, кто хочет научиться строить сечения. Она содержит 11 заданий для построения сечений, подсказки и ответы к каждому заданию. Рекомендую сначала прочитать эту статью и посмотреть это видео.
Вспомним, что сечение многогранника плоскостью представляет собой плоский многоугольник, вершины которого принадлежат сторонам, а ребра — граням многогранника. Две соседние вершины принадлежат одной грани многогранника.
Чтобы найти точку, лежащую одновременно в двух плоскостях, нужно найти точку пересечения прямой, лежащей в первой плоскости, с прямой, лежащей во второй плоскости.
В подсказках и ответах изображение дополнительных прямых, используемых при построении сечения, сплошными линиями или пунктирными, не зависит от того, видимы эти прямые или нет.
Рядом с каждой дополнительной прямой указан ее порядковый номер при построении сечения. Все прямые проведены через две точки, принадлежащие определенной плоскости. Прямые пронумерованы в порядке их построения. Рекомендуется при использовании подсказки и воспроизведении построения сечения проговаривать, какой плоскости принадлежит данная прямая, каким плоскостям принадлежит точка их пересечения.
Постройте сечения, проходящие через точки 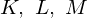 .
.
Задание 1:
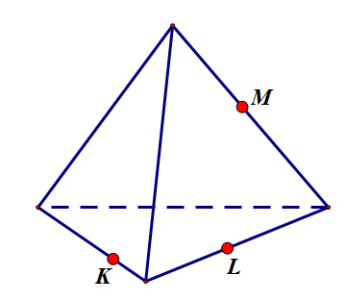
Методы построения сечений многогранников
Разделы: Математика
Метод сечений многогранников в стереометрии используется в задачах на построение. В его основе лежит умение строить сечение многогранника и определять вид сечения.
Данный материал характеризуется следующим особенностями:
- Метод сечений применяется только для многогранников, так как различные сложные (наклонные) виды сечений тел вращения не входят в программу средней школы.
- В задачах используются в основном простейшие многогранники.
- Задачи представлены в основном без числовых данных, чтобы создать возможность их многовариантного использования.
Чтобы решить задачу построения сечения многогранника ученик должен знать:
- что значит построить сечение многогранника плоскостью;
- как могут располагаться относительно друг друга многогранник и плоскость;
- как задается плоскость;
- когда задача на построение сечения многогранника плоскостью считается решенной.
Поскольку плоскость определяется:
- тремя точками;
- прямой и точкой;
- двумя параллельными прямыми;
- двумя пересекающимися прямыми,
построение плоскости сечения проходит в зависимости от задания этой плоскости. Поэтому все способы построения сечений многогранников можно разделить на методы.
Существует три основных метода построения сечений многогранников:
- Метод следов.
- Метод вспомогательных сечений.
- Комбинированный метод.
Первые два метода являются разновидностями Аксиоматического метода построения сечений.
Можно также выделить следующие методы построения сечений многогранников:
- построение сечения многогранника плоскостью, проходящей через заданную точку параллельно заданной плоскости;
- построение сечения, проходящего через заданную прямую параллельно другой заданной прямой;
- построение сечения, проходящего через заданную точку параллельно двум заданным скрещивающимся прямым;
- построение сечения многогранника плоскостью, проходящей через заданную прямую перпендикулярно заданной плоскости;
- построение сечения многогранника плоскостью, проходящей через заданную точку перпендикулярно заданной прямой.
В федеральный перечень учебников по геометрии для 10-11 класов входят учебники авторов:
- Атанасяна Л.С., Бутузова В.Ф., Кадомцева С.Б. и др (Геометрия, 10-11);
- Погорелова А.В. (Геометрия, 7-11);
- Александрова А.Д., Вернера А.Л., Рыжик В.И. (Геометрия, 10-11);
- Смирновой И.М. (Геометрия, 10-11);
- Шарыгина И.Ф. (Геометрия, 10-11).
Рассмотрим подробнее учебники Л.С, Атанасяна и Погорелова А.В.
В учебнике Л.С. Атанасяна на тему “Построение сечений многогранников” выделено два часа. В 10 классе в теме “Параллельность прямых и плоскостей” после изучения тетраэдра и параллелепипеда отводится один час на изложение параграфа “Задачи на построение сечений”. Рассматриваются сечения тетраэдра и параллелепипеда. И тема “Параллельность прямых и плоскостей” завершается решением задач на одном или двух часах (всего задач на построение сечений в учебнике восемь).
В учебнике Погорелова А.В. на построение сечений отводится около трех часов в главе “Многогранники”: один – на изучение темы “Изображение призмы и построение ее сечений”, второй – на изучение темы “Построение пирамиды и ее плоских сечений” и третий – на решение задач. В списке задач, приведенных после темы, задач на сечение насчитывается всего около десяти.
Мы предлагаем систему уроков по теме “Построение сечений многогранников” для учебника Погорелова А.В.
Материал предлагается расположить в той последовательности, в какой он может применяться для обучения учащихся. Из изложения темы “Многогранники” предлагается исключить следующие параграфы: “Построение сечений призмы” и “Построение сечений пирамиды” с тем, чтобы систематизировать данный материал в конце этой темы “Многогранники”. Классифицировать его по тематике задач с примерным соблюдением принципа “от простого к сложному” можно весьма условно следующим образом:
- Определение сечения многогранников.
- Построение сечений призмы, параллелепипеда, пирамиды методом следов. (Как правило в школьном курсе стереометрии используются задачи на построение сечений многогранников, решаемые основными методами. Остальные методы, в связи с их более высоким уровнем сложности, учитель может оставить для рассмотрения на факультативных занятиях или на самостоятельное изучение. В задачах на построение основными методами требуется построить плоскость сечения, проходящую через три точки).
- Нахождение площади сечений в многогранниках (без использования теоремы о площади ортогональной проекции многоугольника).
- Нахождение площади сечений в многогранниках (с применением теоремы о площади ортогональной проекции многоугольника).
СТЕРЕОМЕТРИЧЕСКИЕ ЗАДАЧИ НА ПОСТРОЕНИЕ СЕЧЕНИЙ МНОГОГРАННИКОВ И МЕТОДИКА ИХ ИСПОЛЬЗОВАНИЯ НА УРОКАХ В 10-11 КЛАССАХ.
(система уроков и факультативных занятий по теме “Построение сечений многогранников”)
Тема урока: “Построение сечений многогранников”.
Цель урока: ознакомление с методами построений сечений многогранников.
- Актуализация опорных знаний.
- Постановка задачи.
- Изучение нового материала:
- Подведение итогов урока.
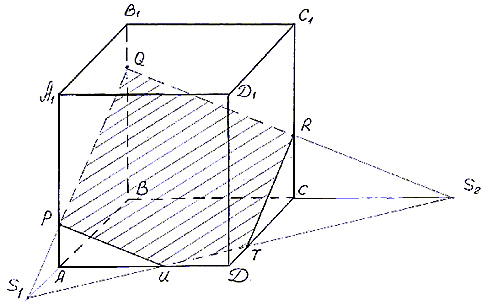
- Построим след секущей плоскости на плоскость нижнего основания призмы. Рассмотрим грань АА1В1В. В этой грани лежат точки сечения P и Q. Проведем прямую PQ.
- Продолжим прямую PQ, которая принадлежит сечению, до пересечения с прямой АВ. Получим точку S1, принадлежащую следу.
- Аналогично получаем точку S2 пересечением прямых QR и BC.
- Прямая S1S2 — след секущей плоскости на плоскость нижнего основания призмы.
- Прямая S1S2 пересекает сторону AD в точке U, сторону CD в точке Т. Соединим точки P и U, так как они лежат в одной плоскости грани АА1D1D. Аналогично получаем TU и RT.
- PQRTU – искомое сечение.
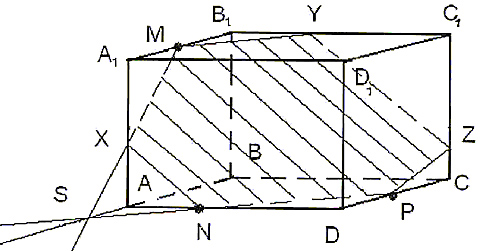
- Точки N и P лежат в плоскости сечения и в плоскости нижнего основания параллелепипеда. Построим прямую, проодящую через эти точки. Эта прямая является следом секущей плоскости на плоскость основания параллелепипеда.
- Продолжим прямую, на которой лежит сторона AB параллелепипеда. Прямые AB и NP пересекутся в некоторой точке S. Эта точка принадлежит плоскости сечения.
- Так как точка M также принадлежит плоскости сечения и пересекает прямую АА1 в некоторой точке Х.
- Точки X и N лежат в одной плоскости грани АА1D1D, соединим их и получим прямую XN.
- Так как плоскости граней параллелепипеда параллельны, то через точку M можно провести прямую в грани A1B1C1D1, параллельную прямой NP. Эта прямая пересечет сторону В1С1 в точке Y.
- Аналогично проводим прямую YZ, параллельно прямой XN. Соединяем Z с P и получаем искомое сечение – MYZPNX.
- Решение задач на нахождение площади сечения:
- Так как основание пирамиды – равносторонний треугольник и точка М – середина стороны, то СМ является высотой и тогда, СМ =
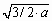 .
. - Площадь треугольника можно найти:
- Поскольку точки Е и F принадлежат плоскости сечения и плоскости грани A1B1C1D1, а две плоскости пересекаются по прямой, то прямая EF будет являться следом секущей плоскости на плоскость грани A1B1C1D1 (рис.8).
- Аналогично получаются прямые ED и FD.
- EDF – искомое сечение.
А) Определение сечения.
Б) Методы построений сечений:
б) метод вспомогательных сечений;
в) комбинированный метод.
Примеры построений сечений методом следов.
Актуализация опорных знаний.
Вспомним:
— пересечение прямой с плоскостью;
— пересечение плоскостей;
— свойства параллельных плоскостей.
Вопросы к классу:
— Что значит построить сечение многогранника плоскостью?
— Как могут располагаться относительно друг друга многогранник и плоскость?
— Как задается плоскость?
— Когда задача на построение сечения многогранника плоскостью считается решенной?
Изучение нового материала.
А) Итак, задача состоит в построении пересечения двух фигур: многогранника и плоскости ( рис.1). Это могут быть: пустая фигура (а), точка (б), отрезок (в), многоугольник (г). Если пересечение многогранника и плоскости есть многоугольник, то этот многоугольник называется сечением многогранника плоскостью.
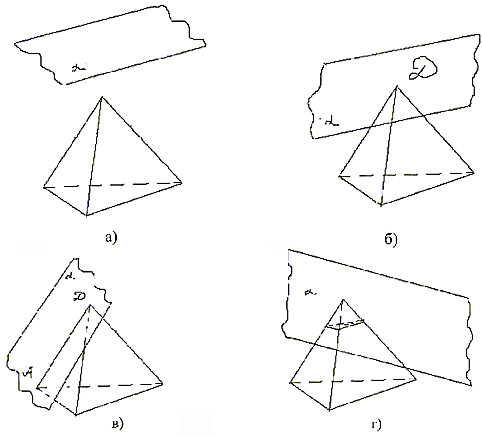
Будем рассматривать только случай, когда плоскость пересекает многогранник по его внутренности. При этом пересечением данной плоскости с каждой гранью многогранника будет некоторый отрезок. Таким образом, задача считается решенной, если найдены все отрезки, по которым плоскость пересекает грани многогранника.
Исследуйте сечения куба (рис.2) и ответьте на следующие вопросы:
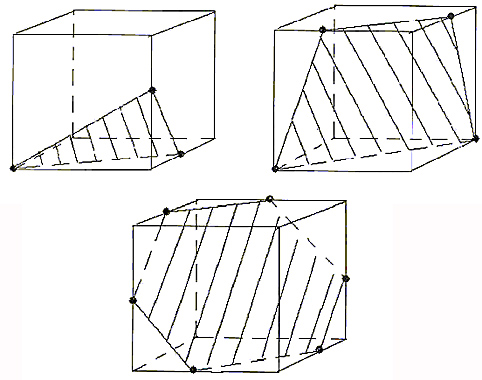
— какие многоугольники получаются в сечении куба плоскостью? (Важно число сторон многоугольника);
[ Предполагаемые ответы: треугольник, четырехугольник, пятиугольник, шестиугольник.]
— может ли в сечении куба плоскостью получиться семиугольник? А восьмиугольник и т.д.? Почему?
Давайте рассмотрим призму и ее возможные сечения плоскостью ( на модели). Какие многоугольники получаются?
Какой можно сделать вывод? Чему равно наибольшее число сторон многоугольника, полученного сечением многогранника с плоскостью?
[ Наибольшее число сторон многоугольника, полученного в сечении многогранника плоскостью, равно числу граней многогранника.]
Б) а) Метод следов заключается в построении следов секущей плоскости на плоскость каждой грани многогранника. Построение сечения многогранника методом следов обычно начинают с построения так называемого основного следа секущей плоскости, т.е. следа секущей плоскости на плоскости основания многогранника.
б) Метод вспомогательных сечений построения сечений многогранников является в достаточной мере универсальным. В тех случаях, когда нужный след (или следы) секущей плоскости оказывается за пределами чертежа, этот метод имеет даже определенные преимущества. Вместе с тем следует иметь ввиду, что построения, выполняемые при использовании этого метода, зачастую получаются “скученными”. Тем не менее в некоторых случаях метод вспомогательных сечений оказывается наиболее рациональным.
Метод следов и метод вспомогательных сечений являются разновидностями аксиоматического метода построения сечений многогранников плоскостью.
в) Суть комбинированного метода построения сечений многогранников состоит в применении теорем о параллельности прямых и плоскостей в пространстве в сочетании с аксиоматическим методом.
А теперь на примере решения задач рассмотрим метод следов.
4. Закрепление материала.
Задача 1.
Построить сечение призмы ABCDA1B1C1D1 плоскостью, проходящей через точки P, Q, R (точки указаны на чертеже (рис.3)).
Построить сечение параллелепипеда ABCDA1B1C1D1 плоскостью, проходящей через точки M, N, P (точки указаны на чертеже (рис.4)).
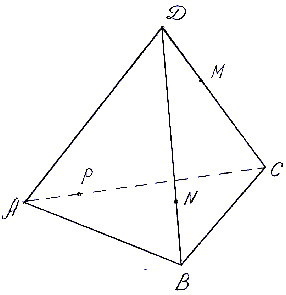
Задача 3 ( для самостоятельного решения).
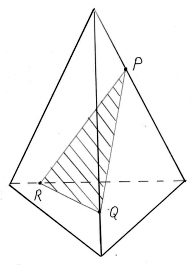
Построить сечение тетраэдра DACB плоскостью, проходящей через точки M, N, P (точки указаны на чертеже (рис.5)).
5. Подведение итогов урока.
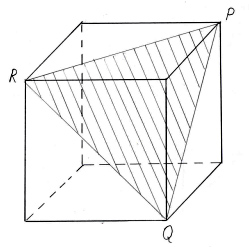
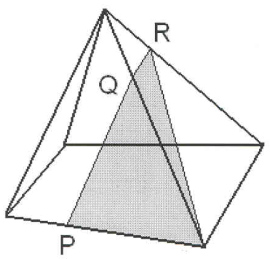
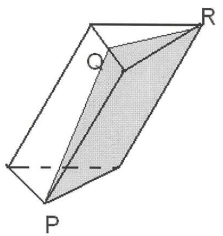
Ответьте на вопрос: являются ли закрашенные фигуры сечениями изображенных многогранников плоскостью PQR? И выполните правильное построение (рис. 6).
Вариант 1.
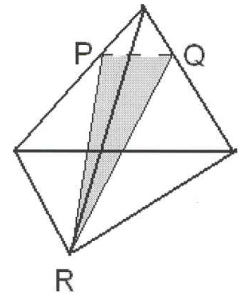
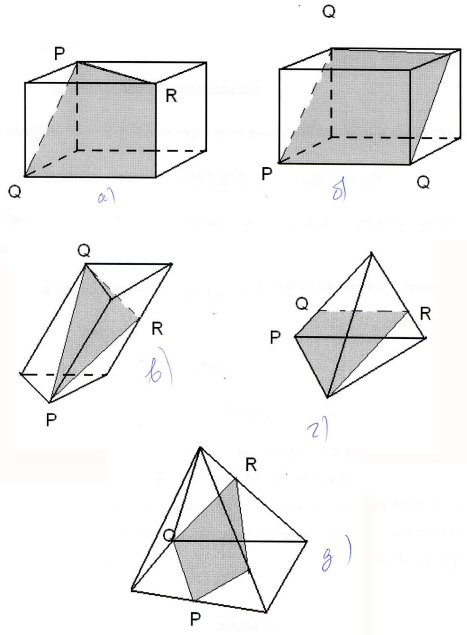
Вариант 2.
Тема урока: НАХОЖДЕНИЕ ПЛОЩАДИ СЕЧЕНИЯ.
Цель урока: познакомить со способами нахождения площади сечения многогранника.
Этапы урока:
-
Актуализация опорных знаний.
Вспомнить теорему о площади ортогональной проекции многоугольника.
— без использования теоремы о площади ортогональной проекции многоугольника;
— с использованием теоремы о площади ортогональной проекции многоугольника.
3. Подведение итогов урока.
-
Актуализация опорных знаний.
Вспомним теорему о площади ортогональной проекции многоугольника: площадь ортогональной проекции многоугольника на плоскость равна произведению его площади на косинус угла между плоскостью многоугольника и плоскостью проекции.
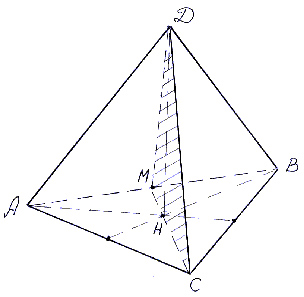
ABCD – правильная треугольная пирамида со стороной основания AB равной а и высотой DH равной h. Постройте сечение пирамиды плоскостью, проходящей через точки D, C и М, где М – середина стороны АВ, и найдите его площадь (рис.7).
Сечением пирамиды является треугольник MCD. Найдем его площадь.
S = 1/2 · DH · CM = 1/2 · 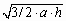 =
= 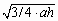
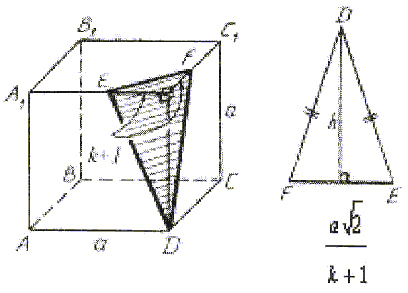
Найти площадь сечения куба ABCDA1B1C1D1 с ребром а плоскостью, проходящей через вершину D и точки Е и F на ребрах А1D1 и C1D1 соответственно, если A1E = k · D1E и C1F = k · D1F.
Построение сечения:

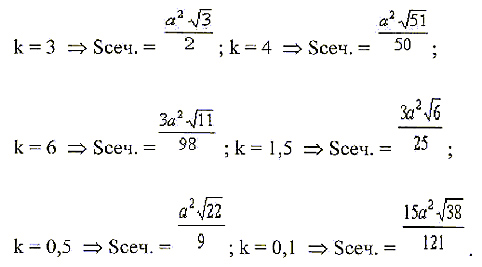
Задача 3 (для самостоятельного решения).
Построить сечение куба ABCDA1B1C1D1 со стороной а плоскостью, проходящей через точки B, M и N, где Ь – середина ребра АА1, а N – середина ребра СС1.
Сечение строим методом следов.
Площадь сечения находим с помощью теоремы о площади ортогональной проекции многоугольника. Ответ: S = 1/2 · a 2 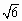 .
.
Правила построения сечение тетраэдра и параллелепипеда.ppt

Кощеев М.М.
МКОУ «Погорельская СОШ».

Цель работы:
Развитие пространственных представлений у учащихся.
Сформировать умения у учащихся строить сечения тетраэдра и
параллелепипеда заданной плоскостью.
Задачи:
Проверить уровень усвоения теоретических знаний по свойствам
параллелепипеда
Формировать у обучающихся навык применения изученных
свойств при решении задач и построений сечений
Рассмотреть возможные варианты сечений тетраэдра и
параллелепипеда.
Познакомить с правилами построения сечений.

На слайде изображена картинка, которую в
детстве нарисовал Экзюпери, будущий
великий писатель и летчик.
Как вы думаете, что изобразил юный
художник?
На самом деле это был удав, проглотивший
слона. Чтобы другие это поняли, юный
художник выразился конкретнее и нарисовал
второй рисунок. Он был уверен, что теперьто
все поймут, так как он объяснил взрослым
свою картинку не только снаружи, но и
изнутри.
Как же это удалось шестилетнему
художнику?
Он мысленно разрезал удава и показал,
что содержится внутри.
Вот и мы, сегодня будем строить
сечения , но не рисунков, а
геометрических фигур тетраэдра и
параллелепипеда

Геометрия является
самым могущественным
средством для изощрения
наших умственных
способностей и дает нам
возможность правильно
мыслить и рассуждать.
Галилео Галилей

Назвать элементы тетраэдра
D
Грань ВСD (4)
Ребро DC (6)
Вершина С (4)
A
C
B

Назвать элементы параллелепипеда
грань A₁B₁C₁D₁ (6)
D1
D
A1
A
C1
B1
ребро СС₁ (12)
Вершина С – (8)
C
Грани оснований:
ABCD — нижнее основание
A₁B₁C₁D₁ — верхнее основание
B

Назвать элементы параллелепипеда
1. Какие две грани называются противоположными,
а какие смежные?
Две грани параллелепипеда, не имеющие общего ребра,
называются противоположными, а имеющие общее ребро
смежными.
2. Какие две вершины называются противоположными?
Две вершины параллелепипеда, не принадлежащие одной
грани, называются противоположными.
3. Что называется диагональю параллелепипеда?
Отрезок, соединяющий противоположные вершины,
называется диагональю параллелепипеда.
4. Что называется измерением параллелепипеда?
Длины трёх рёбер прямоугольного параллелепипеда, имеющих
общую вершину, называют его измерениями

Назвать типы параллелепипедов:
1. Прямоугольный параллелепипед
это параллелепипед, у которого все грани
прямоугольники;
2. Прямой параллелепипед.
это параллелепипед, у которого 4 боковые грани
прямоугольники
3. Наклонный параллелепипед
это параллелепипед, боковые грани которого
не перпендикулярны основанию.
4. Куб
это прямоугольный параллелепипед с равными
измерениями. Все шесть граней куба равные
квадраты.

Общие свойства параллелепипеда
1. Противоположные грани равны и параллельны
2. Диагонали пересекаются в одной точке и делятся этой точкой пополам
Свойства прямоугольного параллелепипеда
1. В прямоугольном параллелепипеде все шесть граней – прямоугольники
2. Все двугранные углы прямоугольного параллелепипеда– прямые
3. Квадрат диагонали прямоугольного параллелепипеда равен сумме
квадратов
трех его измерений. d²=а²+b²+c²
4. Диагонали прямоугольного параллелепипеда равны
5. Полная поверхность прямоугольного параллелепипеда S=2(аb+bc+ас)
Свойства прямого параллелепипеда
1. Боковые грани прямого параллелепипеда — прямоугольники.
2. Диагонали прямого параллелепипеда вычисляются
по формулам: d²=а²+b²+с²+2∙а∙b∙cosα

Устный счет:
Три измерения прямоугольного параллелепипеда
равны 1 см, 2 см, 3 см.
1. Сумма длин всех ребер
равна
24см
2. Сумма площадей всех
его граней равна
S=2(ав+вс+ас)=22см²
3. Длины его диагоналей
равны
d=а²+b²+c²=√14см

Заполнить таблицу
Вариант 1
№ Свойство
1 Основанием этой
фигуры может быть
ромб, не являющийся
квадратом.
2 Все плоские углы
этой фигуры– прямые
3 Все боковые грани
этой фигуры
прямоугольники
4 Противоположные
грани этой фигуры
параллельны и равны
Прямой
паралле
лепипед
Прямоу
гольный
паралле
лепипед
Да
Нет
Нет
Да
Да Да
Да Да
Вариант 2
№ Свойство
1 Противоположные
грани этой фигуры
равны
2 Диагонали этой фигуры
точкой пересечения
делятся пополам
3 К какому виду
предложенных
фигур относится куб
4 Все боковые ребра этой
фигуры
перпендикулярны к
плоскости основания
Прямой
паралле
лепипед
Прямоу
гольный
паралле
лепипед
Да Да
Да Да
Нет
Да
Да Да
Результат: 8 правильных отв. оценка «5», 7правильных отв. оценка «4»,
6 правильных отв. оценка «3», менее 6 правильных отв.

Разминка
гимнастика для глаз
Кабинет, в котором мы занимаемся имеет форму…….
Посмотрите на боковые противоположные грани, на
грани оснований, проведите глазами диагонали с начало
из левой боковой грани, а затем из правой, соедините
глазами вершины фронтальной боковой грани.

Секущей плоскостью многогранника называется
любая плоскость, по обе стороны от которой имеются точки
данного многогранника.
Секущая
плоскость
А
сечение
N
D
Секущая плоскость пересекает грани
многогранника по отрезкам.
Многоугольник, сторонами которого
являются эти отрезки, называется
сечением многогранника.
M
Построить сечение многогранника
плоскостью – это значит
указать точки пересечения
секущей плоскости с ребрами
многогранника и соединить эти
точки отрезками, принадлежащими
граням многогранника.
В
K
С

Какая фигура может быть сечением тетраэдра
Т.к. тетраэдр имеет четыре грани, то в сечении могут
получиться либо треугольники, либо четырехугольники.
Какая фигура может быть сечением параллелепипеда
Т.к. параллелепипед имеет шесть граней, то в сечении могут
получиться треугольники, четырехугольники,
пятиугольники и шестиугольники

Вспомним по готовым рисункам аксиомы и теоремы
стереометрии используемые при построений сечений
А
с
b
α
В
α
Если две точки прямой лежат в
плоскости, то все точки прямой лежат
в этой плоскости.
Через две пересекающиеся прямые
проходит плоскость и притом только
одна
Если две плоскости имеют общую
точку, то они имеют общую прямую, на
которой лежат все общие точки этих
плоскостей.

При построении сечений необходимо
учитывать три правила:
1. Соединять можно только две точки, лежащие в
плоскости одной грани.
2. Секущая плоскость пересекает параллельные грани
по параллельным отрезкам.
3. Если в плоскости грани отмечена только одна точка,
принадлежащая плоскости сечения, то надо построить
дополнительную точку. Для этого необходимо найти
точки пересечения уже построенных прямых с другими
прямыми, лежащими в тех же гранях.
Т.е. Найти пересекающиеся прямые одной плоскости и
построить точку их пересечения
