Решение задач на тему законы сохранения

Примеры решения задач по теме «Закон сохранения механической энергии»

«Физика — 10 класс»

При применении закона сохранения механической энергии для решения задач надо, прежде всего, выяснить, какое состояние системы целесообразно считать начальным, а какое — конечным, затем записать выражение для начальной энергии системы и приравнять его выражению для конечной. При записи потенциальной энергии надо предварительно выбрать нулевой уровень отсчёта потенциальной энергии системы.

Мяч брошен с высоты 1 м под углом 60° к горизонту со скоростью 4 м/с.

Определите максимальную высоту подъёма мяча над поверхностью Земли. Силу сопротивления при движении мяча не учитывайте.

Выберем нулевой уровень потенциальной энергии на поверхности Земли (рис. 5.16). В момент броска в начальном положении 1 мяч обладает кинетической и потенциальной энергиями:

В момент максимальной высоты h_max подъёма скорость мяча направлена горизонтально. Горизонтальная составляющая скорости при движении мяча остаётся постоянной и равной υ_x = υ₀ cosα.

Механическая энергия в положении 2: Е₂ = Е_к2 + Е_п2 = (mυ 2 ₀cos 2 α)/2 + mgh_max.

Так как по условию задачи силой сопротивления можно пренебречь, то считаем, что на мяч действует только консервативная сила — сила тяжести, и, следовательно, полная механическая энергия мяча сохраняется:

Тогда максимальная высота h_mах:

Недеформированную пружину растягивают на Δl = 10 см. Определите работу деформирующей пружину силы и силы упругости пружины, если для растяжения пружины на Δl₀ = 1 см требуется сила F₀ = 2 Н.

Абсолютные удлинения пружины выразим в единицах СИ: Δl₀ = 0,01 м, Δl = 0,1 м. Найдём жёсткость пружины. Из закона Гука F₀ = kΔl₀ следует: k = F₀/Δl₀. Работа деформирующей силы:

Направление силы упругости противоположно направлению деформирующей силы, а по модулю эти силы равны, поэтому A_упр = -1 Дж.

На нити длиной l висит груз. На какую высоту необходимо поднять груз, отклоняя нить от вертикали, чтобы при движении груза вниз без начальной скорости в момент прохождения положения равновесия сила натяжения нити превышала в 2 раза силу тяжести, действующую на груз?

При прохождении нити через вертикальное положение на груз действуют сила натяжения нити и сила тяжести m, лежащие на одной прямой (рис. 5.17). Поэтому ускорение груза является центростремительным и направлено вертикально вверх.

По второму закону Ньютона m = + m.

Запишем этот закон в проекции на ось OY (см. рис. 5.17): Т — mg = mа, где а = υ 2 /l. Учитывая, что Т = 2mg, получаем mg = mа, υ 2 = gl.

Для определения h применим закон сохранения механической энергии, считая, что в положении 2 потенциальная энергия системы «тело—Земля» равна нулю. Тогда в положении 1 система имеет потенциальную энергию Е_п = mgh, где h — высота тела относительно нулевого уровня. В положении 2 тело обладает лишь кинетической энергией Е_к = mυ 2 /2.

По закону сохранения механической энергии mυ 2 /2 = mgh, υ 2 = 2gh. Учитывая, что υ 2 = gl, получаем 2gh = gl, откуда h = 1/2.

Определите скорости двух шаров массами m₁ и m₂ после центрального абсолютно упругого удара. Скорости шаров до удара υ₁ и υ₂ соответственно.

Закон сохранения импульса системы имеет вид

p align=»center»>m₁₁ + m₂₂ = m₁ + m₂₂, (1)

где ₁ и ₂ — скорости шаров после удара.

Запишем уравнение (1) в проекции на ось X (рис. 5.18) (предположим, что шары после удара разлетаются в разные стороны):

Запишем закон сохранения энергии:

Уравнения (2) и (3) образуют систему двух уравнений относительно двух неизвестных u₁ и u₂. Перенесём все члены системы, содержащие m1, в левую часть уравнения, а содержащие m₂, в правую: m₁(υ₁ + u₁) = m₂(υ₂ + u₂), m₁(υ 2 ₁ — u 2 ₁) = m₂(u 2 ₂ — υ 2 ₂).

Очевидно. что u₁ ≠ — υ₁ и u₂ ≠ — υ₂, так как скорости шаров после соударения должны измениться. Разделив левые и правые части равенств одно на другое, получим υ₁ — u₁ = υ₂ — u₂, откуда u₂ = υ₁ + υ₂ — u₁.

Подставив u₂ в уравнение (2), получим уравнение относительно u₁:

Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский

Законы сохранения в механике — Физика, учебник для 10 класса — Класс!ная физика

Решение задач на законы сохранения импульса и энергии (10-й класс)

Разделы: Физика

Цели урока:

Образовательные:

• создание условий для глубокого усвоения системы знаний по законам сохранения в механике;
• закрепление навыков решения физических задач.

Развивающие:

• развитие коммуникативных компетенций в процессе групповой деятельности;
• формировать умения анализировать, устанавливать связи между элементами содержания ранее изученного материала по основам механики,
• развитие познавательных интересов в процессе приобретения знаний и умений по теме.

Воспитательные:

• воспитание понимания необходимости сотрудничества в процессе совместного выполнения задач, уважительного отношения к мнению оппонента при обсуждении проблем естественнонаучного содержания;
• воспитание чувства личной ответственности за результаты совместной деятельности.

Оборудование: компьютер, мультимедийный проектор, доска.

Дидактический материал: карточки-задания для групповой работы.

Задачи урока:

• повторить основные теоретические положения по теме “Законы сохранения в механике”;
• закрепить навыки решения задач.

1. Организационный этап.

2. Повторение закона сохранения импульса (вызвать учащихся к доске).

При взаимодействии тел импульс одного тела может частично или полностью передаваться другому.

3. Рассмотрим примеры. Слайд № 5

При стрельбе из орудия возникает отдача – снаряд движется вперед, а орудие – откатывается назад. Снаряд и орудие – два взаимодействующих тела. Скорость, которую приобретает орудие при отдаче, зависит только от скорости снаряда и отношения масс.

На принципе отдачи основано реактивное движение. В ракете при сгорании топлива газы, нагретые до высокой температуры, выбрасываются из сопла с большой скоростью относительно ракеты. Cлайд № 7

4. Повторим закон сохранения энергии (вызвать учащихся к доске). Cлайд № 8–9

Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой силами тяготения и силами упругости, остается неизменной

А – кинетическая энергия шара;

В – потенциальная энергия шара;

С – полная механическая энергия шара.

5. Решим задачу Х. Гюйгенса: нахождение минимальной прочности легкой нерастяжимой нити, удерживающей тело массой m при его вращении в вертикальной плоскости. Cлайд № 10

6. Закон сохранения механической энергии и закон сохранения импульса позволяют находить решения механических задач в тех случаях, когда неизвестны действующие силы. Примером такого рода задач является ударное взаимодействие тел. Слайд № 11

Ударом (соударением, столкновением) принято называть кратковременное взаимодействие тел, в результате которого их скорости испытывают значительные изменения.

Часто используются две модели ударного взаимодействия –

абсолютно упругий удар

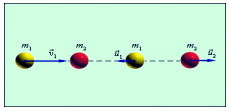
и абсолютно неупругий удар.

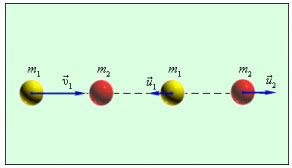
Абсолютно неупругим ударом называют такое ударное взаимодействие, при котором тела соединяются (слипаются) друг с другом и движутся дальше как одно тело.

Абсолютно упругим ударом называется столкновение, при котором сохраняется механическая энергия системы тел.

Во многих случаях столкновения атомов, молекул и элементарных частиц подчиняются законам абсолютно упругого удара.

На основе законов механики математически точно описывается “поведение” бильярдных шаров, столкновения которых друг с другом и со стенками бильярдного стола можно считать абсолютно упругими. Слайд № 13

При этом соударения могут быть центральными и нецентральными

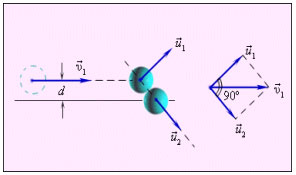
7. Решим задачу: Под каким углом могут разлететься два тела одинаковой массы после упругого нецентрального столкновения? Слайд № 14

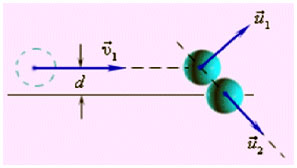
Построим диаграмму импульсов.

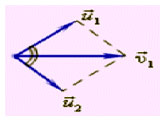
Применим закон сохранения импульса в векторном виде с учётом равенства масс: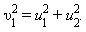

Первое из этих равенств означает, что векторы скоростей образуют треугольник, а второе – что для этого треугольника справедлива теорема Пифагора, то есть он прямоугольный. Искомый угол – это угол между катетами, т.е. он равен 90°.

8. Групповая работа: решение задач по карточкам.

Класс разбивается на несколько групп (в зависимости от количества учащихся), каждой группе даётся карточка с задачами.

9. Проверка решения задач, корректировка решения (по необходимости).

10. Подведение итогов урока, выставление оценок

11. Домашнее задание – оформить решение любой задачи с карточки в виде презентации, подготовить объяснение для класса.

Карточки-задания для групповой работы. (Приложение)

Решение задач по теме Законы сохранения и превращения энергии

Урок 22. Физика 9 класс

Конспект урока «Решение задач по теме Законы сохранения и превращения энергии»

Умение решать задачи —

подобное плаванию или

катанию на лыжах, или

игре на фортепиано:

научиться этому можно,

лишь подражая избранным

образцам и постоянно тренируясь

Ранее были рассмотрены два фундаментальных закона природы — это закон сохранения импульса и закон сохранения энергии.

Закон сохранения импульса гласит, что геометрическая сумма импульсов тел, составляющих замкнутую систему, остается постоянной при любых взаимодействиях тел системы между собой.

Согласно закону сохранения энергии, полная механическая энергия замкнутой системы тел, взаимодействующих силами тяготения, остается постоянной, при любых взаимодействиях в системе.

В данной теме рассмотрим применимость этих законов на практике.

Задача 1. Горизонтально летящая пуля массой 10 г, двигаясь со скоростью 100 м/с, попадает в лежащий на горизонтальном столе брусок массой 100 г и, пробив его, движется со скоростью 90 м/с. Сила трения, действующая на брусок равна 0,11 Н, а время движения пули в бруске составляет 0,001 с. Найти скорость бруска после пробивания его пулей.

Проанализируем процессы, происходящие в ситуации, описанной в задаче.

Выберем систему отсчета связанную с неподвижным бруском. В качестве системы взаимодействующих тел выберем систему «брусок — пуля».

Силы, с которыми пуля действует на брусок, а брусок на пулю, будут внутренними; силы тяжести пули и бруска, сила реакции стола, сила трения, действующая на брусок, — это внешние силы.

На первый взгляд внешние силы не маленькие, система не замкнута, следовательно, закон сохранения импульса не применим.

Двигаясь в бруске, пуля испытывает силу сопротивления, которая меняется по неизвестному закону с изменением скорости, поэтому найдем среднюю силу, с которой брусок действует на пулю. Кроме того, на пулю будет действовать ее сила тяжести.

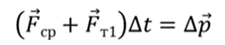
В проекциях на ось Ox:

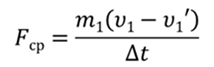
Это средняя сила, с которой брусок действует на пулю.

По третьему закону Ньютона с такой же силой и пуля будет действовать на брусок.

Определим значение внешних сил.

Сила тяжести пули равна

Сила тяжести бруска

Сила реакции опоры в период взаимодействия бруска и пули

Сила трения, из условия задачи, равна

Сравнение значений внешних сил с внутренней показывает, что они намного меньше внутренней силы. Такое относительно большое значение внутренней силы связано с тем, что время взаимодействия очень мало. Такое взаимодействие называют ударным.

Т. о. можно сделать вывод, что при кратковременных (ударных) взаимодействиях тел внутренние силы во много раз превышают внешние, каковыми можно поэтому пренебречь и, считая систему замкнутой, применить закон сохранения импульса.

Запишем закон сохранения импульса

В проекциях на ось координат:

Тогда искомая скорость равна

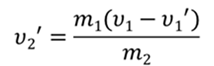
Проанализировав решение задачи, можно получить общий алгоритм решения задач с использованием закона сохранения импульса:

1) выбрать систему отсчета.

2) выделить систему взаимодействующих тел и выяснить, какие силы для нее являются внутренними, а какие внешними.

3) определить импульс всех тел системы до и после взаимодействия.

4) если в целом система незамкнута, но сумма проекций сил на одну из осей равна нулю, то следует написать закон сохранения лишь в проекциях на эту ось.

5) если внешние силы пренебрежимо малы в сравнении с внутренними (как в случае удара тел), то следует написать закон сохранения суммарного импульса в векторной форме и перейти к скалярной.

Теперь выработаем алгоритм решения задач на закон сохранения энергии. Для этого рассмотрим следующую задачу.

Задача 2. Тело брошено с поверхности земли под углом к горизонту с некоторой начальной скорость . Найдите скорость тела на некоторой высоте h, если сопротивление воздуха пренебрежимо мало.

Т.к. по условию задачи сопротивлением воздуха можно пренебречь, то, в данном случае, на тело будет действовать только потенциальная сила — сила тяжести. Значит, к телу можно применить закон сохранения энергии.

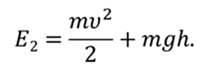
Заметим, что эту задачу можно решить и кинематически, задав угол альфа, но это решение будет во много раз более сложным и громоздким.

Второй закон Ньютона

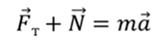
В проекциях на ось Ох:

Алгоритм решения задач на закон сохранения энергии:

1) Выбрать систему отсчета.

2) Выбрать два или более таких состояний тел системы, чтобы в число их параметров входили как известные, так и искомые величины.

3) Выбрать нулевой уровень отсчета потенциальной энергии.

4) Определить, какие силы действуют на тела системы — потенциальные или не потенциальные.

5)Если на тела системы действуют только потенциальные силы, записать закон сохранения механической энергии.

6) Раскрыть значения энергии в каждом состоянии и, подставив их в уравнение закона сохранения энергии, решить уравнение относительно искомой величины.

Решение задач на тему законы сохранения

Кандидат физико-математических наук В. ПОГОЖЕВ.

Число желающих поступить в высшие учебные заведения инженерного и физико-математического профиля год от года растет. Материалы одной из старейших рубрик журнала дают ясное представление об уровне сложности задач по физике, ожидающих абитуриентов на вступительных экзаменах. Продолжаем публиковать разбор типовых конкурсных задач по физике, в разные годы предлагавшихся поступающим на физический факультет МГУ им. М. В. Ломоносова, начатый в № 3 журнала за этот год.

Применение законов сохранения энергии и импульса часто позволяет получать решение наиболее простым и изящным образом, избавляя от громоздких и утомительных расчетов. И совершенно необходимым оказывается их применение, когда законы взаимодействия тел неизвестны или описание поведения механической системы с помощью уравнений движения приводит к столь сложным соотношениям, что получить окончательное решение практически невозможно. Вместе с тем законы сохранения никогда не дают и не могут дать однозначного ответа на вопрос о том, что происходит. Но если, исходя из каких-либо других соображений, можно указать, что именно должно произойти , то законы сохранения дают ответ на вопрос, как это произойдет.

Программа вступительных экзаменов в вузы предусматривает знание абитуриентами законов сохранения импульса и механической энергии. Эти частные случаи законов изменения импульса и механической энергии могут быть доказаны с помощью законов Ньютона. Не повторяя вывода, имеющегося в школьных учебниках, напомним только их формулировки.

Закон изменения импульса: приращение импульса механической системы относительно инерциального наблюдателя за некоторый промежуток времени равно импульсу внешних сил, действовавших на тела системы, за тот же промежуток времени. Следовательно, если импульс внешних сил, действовавших на тела системы, за рассматриваемый промежуток времени равен нулю, то импульс системы в конечный момент указанного промежутка времени будет равен импульсу системы в начальный момент. Такая формулировка является и достаточной и необходимой. Однако в таком виде закон сохранения импульса обычно не формулируют, так как проверить выполнимость указанного условия при неизвестном характере сил взаимодействия тел системы с внешними телами невозможно, а при известном задачу проще решить, не используя закон сохранения. Вместе с тем очевидно, что если сумма внешних сил, действующих на тела системы, в любой момент времени равна нулю (такую систему называют замкнутой), то импульс системы будет оставаться постоянным относительно любого инерциального наблюдателя в течение этого промежутка. Учитывая векторный характер фигурирующих в законе величин, можно утверждать, что при равенстве нулю суммы проекций внешних сил на некоторое направление в течение определенного времени проекция импульса системы на это направление будет оставаться неизменной при любых процессах в этой системе в указанный промежуток времени. Более того, если требуется определить изменение характера движения частей системы (а не системы в целом!) и известно, что силы взаимодействия этих частей во много раз превышают внешние силы, действующие на них, можно пренебречь действием внешних сил, то есть считать систему замкнутой. Обычно такая ситуация имеет место при взрывах, выстрелах и других подобных процессах. Однако при этом необходимо убедиться, что внешние силы все время остаются достаточно малыми.

Закон изменения механической энергии: приращение механической энергии системы тел относительно инерциального наблюдателя равно сумме работы внешних сил над телами системы и работы внутренних неконсервативных сил за рассматриваемый промежуток времени. Следовательно, если система изолирована (ни на одну ее точку не действуют внешние силы), а внутренние силы консервативны , ее механическая энергия относительно инерциального наблюдателя не зависит от времени. Приведенная формулировка закона сохранения механической энергии достаточна, но не необходима. Так, если в изолированной системе наряду с консервативными действуют силы сухого трения покоя, суммарная работа сил трения в силу третьего закона Ньютона равна нулю, и механическая энергия такой системы остается неизменной. Еще раз обратим внимание, что в приведенной формулировке закона сохранения механической энергии содержится требование изолированности, а не только замкнутости рассматриваемой системы тел.

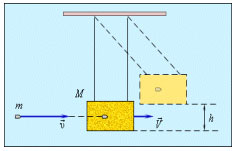
Задача 1 (2000 г.). На тонкостенный обод заторможенного велосипедного колеса, ось которого расположена горизонтально и закреплена, намотана тонкая нерастяжимая нить. Один конец нити прикреплен к ободу, а на другом конце висит груз массой m. Радиус колеса равен R, масса обода равна М. Пренебрегая трением, массой спиц, втулки и нити, найти величину ускорения A точек обода колеса через промежуток времени t после отпускания колеса, если в течение этого промежутка груз двигался поступательно.

Эта и следующая задачи трудны тем, что в программе вступительных экзаменов нет упоминания об уравнении динамики вращательного движения протяженных тел. Однако эти и подобные им задачи легко решаются с помощью закона сохранения механической энергии.

Решение. Будем считать лабораторную систему отсчета, в которой ось обода неподвижна, инерциальной. По условию обод недеформируемый, а нить нерастяжима. Поэтому можно утверждать, что в тот момент времени t, когда скорость груза становится равной v(t), точно такую же по величине линейную скорость должна иметь и любая точка тонкого обода. Как известно, кинетическая энергия материальной точки массой m, движущейся относительно инерциального наблюдателя со скоростью v, равна mv 2 /2, а кинетическая энергия системы точек равна сумме их кинетических энергий. Поэтому, пренебрегая в соответствии с условием задачи массой нити, спиц и втулки, можно считать, что в указанный момент времени кинетическая энергия системы «колесо — нить — груз — Земля» должна стать равной (M+m)v 2 /2. При этом мы считаем, что кинетическая энергия Земли при опускании груза остается неизменной. Последнее утверждение может показаться неверным. Действительно, если пренебречь влиянием на рассматриваемые тела других тел, указанную систему следует считать изолированной. Следовательно, поскольку импульс вращающегося вокруг неподвижной оси однородного твердого обода равен нулю, импульс нити тоже равен нулю (по условию задачи нить невесома), то на основании закона сохранения импульса нужно считать, что приращения импульсов груза и Земли по отношению к инерциальной системе отсчета должны быть одинаковыми по величине. Однако учитывая, что масса Земли во много раз больше массы груза, изменением скорости Земли по отношению к инерциальной системе отсчета, обусловленным движением груза, и ее кинетической энергией следует пренебречь. То есть действительно лабораторную систему можно считать инерциальной, а согласно условию — и консервативной. Поэтому на основании закона сохранения механической энергии можно утверждать, что приобретенная системой к моменту времени t кинетическая энергия равна убыли ее потенциальной энергии, обусловленной опусканием груза на высоту h. Очевидно, возможные перемещения груза малы по сравнению с радиусом Земли, а потому действующую на груз силу тяжести mg необходимо считать постоянной. Тогда из сказанного следует, что в любой допустимый по условию задачи момент времени t должно иметь место соотношение

(М + m) υ 2 (t) / 2 = m g h (t).

Поскольку на груз со стороны Земли действует не зависящая от положения груза сила тяжести и согласно сказанному выше величина тангенциальной составляющей ускорения точек обода a_τи величина ускорения груза а должны быть равны, можно считать, что в любой момент времени t ускорение груза остается неизменным. Поэтому можно утверждать, что

υ (t) = at и h (t) = at 2 / 2.

Подставив эти соотношения в предыдущее уравнение, получим

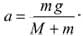
Учитывая, наконец, что нормальная составляющая ускорения точки, движущейся по окружности радиусом R со скоростью v, равна a_n = υ 2 / R и направлена перпендикулярно тангенциальной составляющей ее ускорения, определим искомое ускорение точек обода колеса в заданный момент времени t = τ:

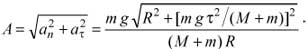
Задача 2 (2000 г.). Однородное тонкостенное кольцо массой m скатывается без проскальзывания по закрепленному желобу так, что его плоскость все время остается в плоскости вертикального сечения желоба, имеющего форму дуги окружности радиусом R. Радиус кольца r много меньше R. Найти силу, с которой кольцо будет действовать в нижней точке на желоб, если на высоте h = R/2 от этой точки кольцо имело скорость v.

Решение. При решении задачи будем, как обычно, пренебрегать влиянием воздуха на движение кольца. Поскольку кольцо скатывается без проскальзывания, то величина скорости v центра кольца и угловая скорость его вращения относительно горизонтальной оси, проходящей через центр кольца перпендикулярно его плоскости, должны удовлетворять соотношению v=wr. Отсюда с учетом того, что кольцо тонкое, следует, что скорость любой i-той точки кольца v_i=v+v_iвр, где v_iвр — скорость этой точки относительно центра кольца. Поэтому кинетическая энергия катящегося без проскальзывания кольца должна быть равна:

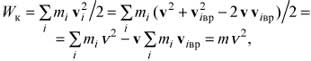
так как массы диаметрально противоположных точек кольца m_i в силу его однородности равны, а их скорости, обусловленные вращением колеса вокруг своей оси, равны по величине, но противопо ложны по направлению.

Поскольку кольцо скатывается без проскальзывания, действующая на него со стороны желоба сила сухого трения является силой трения покоя, и ее работа над кольцом и желобом равна нулю. Поэтому, если, как обычно, считать систему «кольцо — желоб — Земля» изолированной и пренебречь силами трения качения, можно утверждать, что для нее должен выполняться закон сохранения механической энергии. Учитывая, что масса Земли во много раз больше массы кольца, изменение ее скорости при движении кольца пренебрежимо мало, поэтому лабораторная система инерциальна (см. решение предыдущей задачи). Тогда, с учетом сказанного ранее, можно утверждать, что приращение кинетической энергии рассматриваемой системы тел должно быть равно убыли ее потенциальной энергии. Если скорость кольца в нижней точке траектории обозначить v_н, приращение его кинетической энергии при скатывании до нижней точки желоба

При этом убыль потенциальной энергии системы, считая ускорение свободного падения g постоянным и учитывая, что по условию задачи h = R/2 >> r, будет ∆ W_п = (h — r) mg

mgR/2. Из сказанного следует, что в нижней точке траектории скорость кольца должна стать

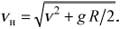
Поскольку в этой точке ускорение кольца направлено вертикально вверх и равно v_н 2 /R, тангенциальная составляющая действующей на кольцо силы реакции желоба (сила сухого трения покоя) равна нулю, а нормальная составляющая N указанной силы, согласно второму закону Ньютона, должна быть равна (g+v_н 2 /R) m. Следовательно, согласно третьему закону Ньютона, искомая сила, с которой кольцо действует на желоб, равна

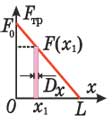
Задача 3 (1999 г.) Длинная трубка, запаянная с одного конца, наполнена ртутью и закрыта легкой пробкой, касающейся ртути, но не оказывающей на ртуть никакого давления. Внутри трубки находится часть пробки длиной L. Масса ртути равна m, площадь поперечного сечения трубки — S, атмосферное давление — р_а. Удерживая пробку, трубку поворачивают отверстием вертикально вниз. После этого пробку отпускают, и она вылетает из удерживаемой неподвижной трубки. Зная, что сила трения, действующая на пробку со стороны трубки, изменяется по закону F = (1 — x/L)F ₀, где х — длина участка пробки, вышедшего из трубки, найти скорость пробки в момент ее вылета. Силами трения ртути пренебречь.

Решение. При решении задачи будем считать, что в момент отпускания пробки трубка вместе с ее содержимым покоилась относительно лабораторной системы отсчета, которую будем считать инерциальной.

Применим закон изменения механической энергии к системе «ртуть — пробка». По условию задачи массой пробки и силами вязкого трения ртути о стенки трубки следует пренебречь и считать, что в исходном состоянии пробка не действует на ртуть. Поэтому после переворачивания со стороны стенок и дна трубки на ртуть действуют только силы, направленные горизонтально. Тогда на основании закона изменения механической энергии можно утверждать, что приращение кинетической энергии ртути и пробки равно, с одной стороны, приращению лишь кинетической энергии ртути, а с другой — работе сил тяжести, действующих на ртуть, сил атмосферного давления и сил трения, действующих на пробку. Поскольку после отпускания пробка вылетает из трубки, можно утверждать, что максимальная величина силы трения, действующей на пробку, удовлетворяет неравенству 0 2 / 2, где v — искомая скорость вылета пробки из трубки. Пренебрегая изменением атмосферного давления и ускорения свободного падения g при перемещении пробки на расстояние L, можно считать, что силы тяжести совершат над пробкой и ртутью положительную работу, равную A = mgL, работа же сил атмосферного давления будет отрицатель ной и равной A_ат= — p_aSL, так как направление результирующей силы атмосферного давления противоположно направлению перемещения пробки.

Вычислить величину работы силы трения, действовавшей на пробку со стороны трубки, можно с помощью рисунка, на котором показана зависимость величины этой силы от длины х вышедшего из трубки участка пробки. По определению элементарная работа изменяющейся силы F при столь малом (элементарном) перемещении Dr точки ее приложения, что силу на этом перемещении можно считать постоянной как по величине, так и по направлению относительно ∆r, равна ∆A = F∆r. В соответствии с этим элементарная работа силы трения при перемещении пробки на малое расстояние , когда из трубки вышла часть пробки длиной , по модулю равна площади затененного на рисунке прямоугольника. Поэтому величина всей работы сил трения будет равна площади треугольника F₀0L, то есть F₀ L/2. Таким образом, искомая скорость должна удовлетво рять соотношению

mυ 2 / 2 = mgL — p_aSL — F₀L / 2